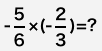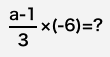数学
2026.02.01
キーボードを使って解く方法(1)
0-0-0-0
キーボードを使って解く方法
ログイン
この問題は、答えを自分で入力する問題です。
解答欄に「さいたま」と入力してみましょう。
入力が終わったら、「Enterキー(エンターキー)」を押しましょう。
「Enterキー」を押すと、次の問題に進みます。

小学校の復習(9)
0-1-1-1
算数クイズ
ログイン
奇数をすべて選びましょう。
0-1-1-2
分数と小数の変換
ログイン
0-1-1-3
計算のきまり
ログイン
計算のきまりを使って計算しましょう。
0-1-1-4
約数と最大公約数
ログイン
この整数の約数を、すべて選びましょう。
9
0-1-1-5
約分
ログイン

0-1-1-6
公倍数と通分
ログイン
この2つの整数の最小公倍数はなんですか?
(2,3)
0-1-1-7
分数の計算
ログイン

0-1-1-8
単位の変換
ログイン
2km= ? m
0-1-1-9
割合
ログイン
400円の1割はいくら?
正負の数(9)
1-1-1-1
正負の数、自然数、整数
ログイン
正の数はどれですか?(すべて)
4 , -2.3 , -2 , 0 , 20 , -14
1-1-1-2
0より大きい数小さい数
ログイン
0より4大きい数を符号を使って表しましょう。
1-1-1-3
数直線①(数直線上の数)
ログイン
xの数を答えましょう。
1-1-1-4
反対の量を表す①
ログイン
3000円の収入(しゅうにゅう)を+3000円とあらわす時、
2000円の支出(ししゅつ)はどうあらわせますか?
1-1-1-5
反対の量を表す②(反対の言葉に変える)
ログイン
[ ]内のことばに変えて、同じ意味を表しましょう。
5cm長い [短い]
1-1-1-6
絶対値
ログイン
+4の絶対値はいくつですか?
1-1-1-7
数直線②(数の範囲・数直線あり)
ログイン
-2 より大きく 2 より小さい整数は
いくつありますか?

1-1-1-8
数直線③(数の範囲・数直線なし)
ログイン
-2 より大きく 2 より小さい整数はいくつありますか?
1-1-1-9
混合問題
ログイン
自然数はどれですか?(すべて)
4 , -2.3 , -2 , 0 , 20 , -1
数の大小(6)
1-1-2-1
不等号を入れる
ログイン
?に当てはまる不等号を入れましょう。
1-1-2-2
分数小数の大小・ヒント付
ログイン
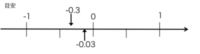
-0.3 ? -0.03
1-1-2-3
分数小数の大小・ヒント無
ログイン
?に当てはまる不等号を入れましょう。
1-1-2-4
3つの数の大小・整数小数
ログイン
次の3つの数の大小を表したもので正しいものを選びましょう。
+1, -3, 0
1-1-2-5
数直線をつかって
ログイン
3 より 2 大きい数は?
![]()
1-1-2-6
混合問題
ログイン
?に不等号を入れましょう。
正負の数の加法・減法(10)
1-1-3-1
同符号の加法・図付
ログイン
(+2)+(+3)=?
![]()
![]()
![]()
![]()
![]()
1-1-3-2
同符号の加法
ログイン
(+3)+(+4)=?
1-1-3-3
異符号の加法・図付
ログイン
(+4)+(-1)=?


1-1-3-4
異符号の加法
ログイン
(+6)+(-3)=?
1-1-3-5
小数と分数の加法
ログイン
(-3.2)+(-1.3)=?
1-1-3-6
混合問題(加法)
ログイン
(-9)+(+9)=?
1-1-4-1
減法(符号を変える)
ログイン
?に当てはまる正負の数を入れましょう。
1-1-4-2
減法の計算
ログイン
(-6)-(+9)=?
1-1-4-3
分数・小数の減法
ログイン
(-1.3)-(-1.3)=?
1-1-4-4
混合問題(減法)
ログイン
?に当てはまる正負の数を入れましょう。
(+7)-(+2)=(+7)+(?)
加減法のまとめ(4)
1-1-5-1
カッコを省いた式(カッコをはずす)
ログイン
カッコを外しましょう。例 (+2)-(-3) → 2+3
(+3)+(-7)
1-1-5-2
カッコを省いた式(カッコを外した式)
ログイン
6-10=?
1-1-5-3
正負の数の加減のまとめ(整数・小数)
ログイン
-7+5+8-4=?
1-1-5-4
正負の数の加減のまとめ(分数)
ログイン
正負の数の乗除(7)
1-1-6-1
正負のかけ算
ログイン
(+3)×(+4)=?
1-1-6-2
逆数
ログイン

1-1-6-3
分数の乗除
ログイン
1-1-6-4
累乗
ログイン
3²=?
1-1-6-5
3つ以上の数の乗除①
ログイン
3×(-2)×(-4)=?
1-1-6-6
3つ以上の数の乗除②(累乗含む)
ログイン
(-3)²×(-2)³=?
1-1-6-7
混合問題
ログイン
(+3)×(+4)=?
四則計算と利用(6)
1-1-7-1
四則計算の計算順序
ログイン
-5²÷(-5)+(-12)
= ? ÷(-5)+(-12)
1-1-7-2
四則計算の基本
ログイン
-6-2×(-3)=?
1-1-7-3
カッコを含んだ計算の順序
ログイン
(5-2)²×(-5)+4
=?²×(-5)+4
1-1-7-4
カッコを含んだ計算
ログイン
(7-4)²×(-5)+4³=?
1-1-8-1
数の範囲
ログイン
-2,5,12,などの数の集まりを、何と言いますか?
1-1-8-2
正負の数の利用
ログイン
この表はある中学2年生の5人の身長をあらわした表です。
![]()
Dの身長はいくつですか?
素数(3)
1-1-9-1
素数の考え方
ログイン
もっとも小さい素数を選びましょう。
1-1-9-2
素因数分解
ログイン
12を素因数分解しましょう。
1-1-9-3
素因数分解
ログイン
12にできるだけ小さい自然数nをかけて、
ある自然数の2乗になるとき、自然数nを求めましょう。
数量を文字で表す(10)
1-2-1-1
数量を文字で表すこと
ログイン
同じ値段のみかんを5個買います。
みかん1個の値段を □ 円として
代金を式に表したものを選びましょう
。
代金を式に表したものを選びましょう
1-2-2-1
積の表し方
ログイン
文字式のきまりにしたがって書き直しましょう。
a×b
1-2-2-2
商の表し方
ログイン
文字式のきまりにしたがって書き直しましょう。
x÷3
1-2-2-3
乗除のまざった式
ログイン
文字式のきまりにしたがって書き直しましょう。
a×2÷b
1-2-2-4
文字式に×,÷を戻す
ログイン
次の式を、記号 × , ÷ を使って書き直しましょう。
4b
1-2-2-5
混合問題
ログイン
文字式のきまりにしたがって書き直しましょう。
a×b
1-2-3-1
個数・代金・位
ログイン
次の数量を表す式を書きましょう。(文字式のきまりを使ってください)
1個 a 円のりんご4個を買ったときの代金
1-2-3-2
距離・速さ・時間
ログイン
次の数量を表す式を書きましょう。(文字式のきまりを使ってください)
時速 5km で a 時間歩いたときの道のり
1-2-3-3
割合
ログイン
次の数量を表す式を書きましょう。(文字式のきまりを使ってください)
a 円の3割
1-2-3-4
混合問題
ログイン
次の数量を表す式を書きましょう。(文字式のきまりを使ってください)
1個 a 円のりんご3個と、1個 b 円のみかん5個を買ったときの代金
式の値1(2)
1-2-4-1
式の値①(文字1つ)
ログイン
x の値が次の場合に、10-2xの値を求めましょう。
x=4
1-2-4-2
式の値②(文字2つ)
ログイン
x=3 y=4 のとき、2x+3yの値を求めましょう。
文字の項をまとめる(6)
1-2-5-1
項・係数はどれ?
ログイン
x+2y-3 の項はどれですか?すべて選びましょう
1-2-6-1
答えの項が一つの問題
ログイン
5a-2a=?
1-2-6-2
答えの項が二つの問題
ログイン
4x-3-2x+2=?
1-2-6-3
カッコを外す問題
ログイン
4x+(2x-2)=?
1-2-6-4
一次式の加減
ログイン
(4x-3)+(2x-2)=?
1-2-6-5
混合問題
ログイン
-5x-2x=?
文字式の乗法・除法(7)
1-2-7-1
乗法・除法
ログイン
2a×3=?
1-2-7-2
項が2つ以上の式にかける
ログイン
5(x-8)=?
1-2-7-3
項が2つ以上の式をわる
ログイン
(20x-10)÷5=?
1-2-7-4
分数の式に数をかける
ログイン
1-2-7-5
いろいろな計算
ログイン
2(a+3)-(3a-1)=?
1-2-7-6
いろいろな計算・分数
ログイン
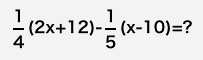
1-2-7-7
混合問題
ログイン
2a×3=?
関係をあらわす式(2)
1-2-8-1
関係をあらわす式①(等式)
ログイン
次の関係を等式にし右辺を埋めましょう。
x の3倍は y より 5 大きい。
3x=
1-2-8-2
関係をあらわす式②(不等式)
ログイン
次の関係を不等式で表したものを選びましょう。
x+3 は 8 より小さい。
方程式の解き方(11)
1-3-1-1
方程式と解
ログイン
次の方程式のうち、3が解であるものはどれですか?
すべて選びましょう。
1-3-2-1
等式の性質
ログイン
次の①の式から②の式に変形するとき
等式の性質のどれを使っていますか?
① x-4=-2
② x=2
1-3-3-1
4x=2などの練習
ログイン
次の方程式を解きましょう。
3x=9
1-3-3-2
xが左辺のみの問題
ログイン
x=?
x+4=9
1-3-3-3
両辺にxがある式
ログイン
x=?
6x-14=4x+2
1-3-3-4
かっこがある式
ログイン
x=?
6x-3(x+4)=-6
1-3-3-5
小数・分数の式の準備
ログイン
次の①の式から②の式に変形するとき
等式の性質のどれを使っていますか?
① 0.2x-0.6=-1.2
② 2x-6=-12
1-3-3-6
小数の方程式
ログイン
x=?
0.9x-6=1.3x+2
1-3-3-7
分数の方程式
ログイン
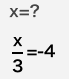
1-3-3-8
混合問題
ログイン
x+4=9
1-3-4-1
比の値と比例式
ログイン
次の比の値はいくつですか?
3:4
方程式の利用(6)
1-3-5-1
代金と個数、ある数
ログイン
2000円でケーキ4個と150円のシュークリーム4個を買うとおつりは200円だった。
ケーキ1個の値段はいくらですか?
1-3-5-2
合わせて何個?
ログイン
2000円で300円のケーキと150円のシュークリームを、
合わせて8個買うとおつりは200円だった。
ケーキとシュークリームそれぞれ何個ずつ買いましたか?
1-3-5-3
過不足の問題
ログイン
何人かの子どもに、みかんを同じ数ずつ分けます。
5個ずつ分けると12個余り、7個ずつ分けると4個たりません。
子どもの人数は何人でしょうか?
1-3-5-4
速さ・時間・道のり
ログイン
妹が、2km離れた友人の家に向かって、家を出発しました。
それから10分たって、兄が妹を自転車で追いかけました。
妹は分速80m、兄は分速240mで進むとすると、
兄は出発してから何分後に妹に追いつくでしょうか。
1-3-5-5
比例式
ログイン
スポンジケーキをつくるために、小麦粉と砂糖を 4:3の割合でまぜる。
小麦粉を160g使うとき砂糖は何g必要ですか?
1-3-5-6
混合問題
ログイン
2000円でケーキ4個と150円のシュークリーム4個を買うとおつりは200円だった。
ケーキ1個の値段はいくらですか?
比例の式(10)
1-4-1-1
関数ですか?
ログイン
次のことがらで y は x の関数であると言えますか?
ある町で、最高気温が x℃ のとき、最低気温は y℃ である。
1-4-1-2
関数の変域
ログイン
x の変域が次の表のような値をとるとき、
x の変域を不等号を使って表しましょう。
※白◯はその数を含まない

1-4-2-1
比例の式はどれ?
ログイン
次の中から比例の式をすべて選び記号で答えましょう。
1-4-2-2
比例の表
ログイン
yはxに比例しています。
アに当てはまる数はなんでしょうか?

1-4-2-3
比例定数
ログイン
この比例の表の比例定数は何ですか?

1-4-2-4
表から式
ログイン
この表からyをxの式(y=ax)を表しましょう。

1-4-2-5
文章から比例の式を読み取る
ログイン
水そうに毎分 6Lの割合で水を入れます。
入れている時間を x分、たまった水の量を yLとします。
そのとき、y は x に比例していると言えますか?
1-4-2-6
x,y の値から式を求める
ログイン
y が x に比例し、x=3 y=6 のとき、
y を x の式 (y=ax) で表しましょう。
1-4-2-7
x,y の値から別の x,y の値を求める
ログイン
y が x に比例し、x=3 y=6 のとき、
y=-18のときの xの値を求めましょう。
1-4-2-8
混合問題
ログイン
次の中から比例の式をすべて選び記号で答えましょう。
比例のグラフ(5)
1-4-3-1
座標①(図から座標)
ログイン
点Aの座標を答えましょう。
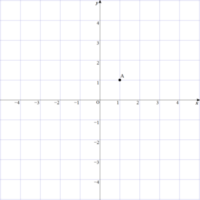
1-4-3-2
座標②(グラフに描けるかの確認)
ログイン
次の座標を、グラフに書き入れましょう。
(2,1)
1-4-4-1
表からグラフが描けるか確認
ログイン
次の表に当てはまるグラフを書きましょう。

1-4-4-2
式からグラフが描けるか確認
ログイン
次の式のグラフを描きましょう。
y=2x
1-4-4-3
グラフから式を求める
ログイン
このグラフの式を求めましょう。
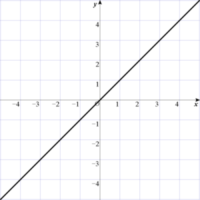
反比例の式とグラフ(8)
1-4-5-1
反比例の式はどれ?
ログイン
次の中から反比例の式をすべて選び記号で答えましょう。
1-4-5-2
反比例の表
ログイン
アに当てはまる数はなんでしょうか?

1-4-5-3
比例定数を求める
ログイン
次の式の比例定数は何ですか?
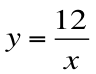
1-4-5-4
表・xyから式を求める
ログイン
この表からyをxの式を表しましょう。

1-4-5-5
x,y の値から別の x,y の値を求める
ログイン
y が x に反比例し、x=3 y=10 のとき、y=5のときの xの値を求めましょう。
1-4-5-6
混合問題
ログイン
次の中から反比例の式をすべて選び記号で答えましょう。
1-4-6-1
式からグラフ
ログイン
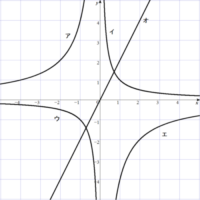
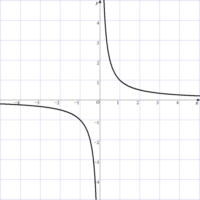
1-4-6-2
グラフから式
ログイン
このグラフの式(y=a/x)を求めましょう。
比例・反比例(5)
1-4-7-1
比例・反比例のグラフから式
ログイン
アのグラフの式を求めましょう。

1-4-7-2
比例・反比例の式の混合問題
ログイン
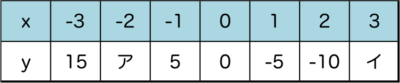
ア、イに当てはまる数はなんでしょうか?
1-4-8-1
比例か反比例か
ログイン
次の文章の y を x の式で表したとき、その式は比例ですか?反比例ですか?
毎日 5km ずつランニングをするとき、x 日間で走った合計の距離は y である。
1-4-8-2
比例の利用
ログイン
次の文章の y を x の式で表しましょう。
一本 30 円のえんぴつ x 本買った時の代金は y 円になります。
1-4-8-3
反比例の利用
ログイン
次の文章の y を x の式で表しましょう。
横が x cm 縦が y cm の長方形の面積が 46cm² である。
図形(4)
1-5-1-1
直線と垂直・平行
ログイン
この図の名前はなんでしょうか?
1-5-1-2
角と三角形
ログイン
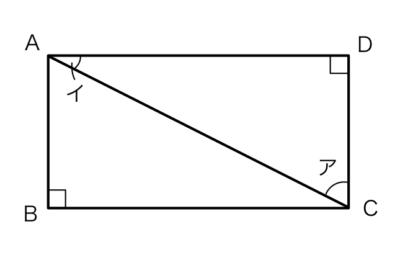
アの角を記号を使って正しく表したものはどれですか?
1-5-2-1
移動した図形はどれ?
ログイン
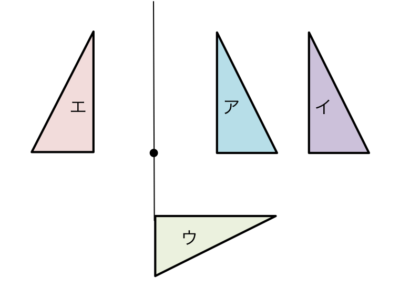
イはアをどのように移動したものでしょうか?
1-5-2-2
図形の移動を描けるかの確認
ログイン
△ABCを矢印の方向に、平行移動した△A’B’C’を描けますか?
作図(5)
1-5-3-1
作図のルールと種類
ログイン
中学の数学の作図を行う時に筆記用具以外で使用する道具はこのうちどれですか?(すべて)
1-5-3-2
作図が描けるかの確認
ログイン
垂直二等分線を引けますか?
1-5-3-3
作図の特徴
ログイン
x=?

1-5-4-1
どの作図を使うか
ログイン
x=?

1-5-4-2
角度の作図の確認問題
ログイン
∠AOB=45°となるような点Aを描けますか?
おうぎ形(7)
1-5-5-1
各部の名称
ログイン
?の名前は?

1-5-5-2
おうぎ形と円の割合
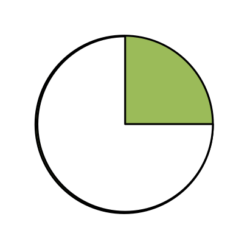
ログイン
色のついているおうぎ形は、円全体の1/4の大きさです。
中心角は何°でしょうか?
1-5-6-1
おうぎ形の弧の長さ
ログイン
下の図の色のついているおうぎ形は半径 4cm、
中心角は90°です。
弧の長さを求めましょう。

1-5-6-2
おうぎ形の面積
ログイン
下の図の色のついているおうぎ形は半径 4cm、
中心角は90°です。
おうぎ形の面積を求めましょう。

1-5-6-3
弧の長さと面積(混合・図なし)
ログイン
半径10cm、中心角108°のおうぎ形の弧の長さを求めましょう。
1-5-7-1
おうぎ形の中心角①(図・円周あり)
ログイン
下の図は円周が8πcm、
色のついているおうぎ形の弧の長さが2πcmです。
おうぎ形の中心角は何°でしょう?

1-5-7-2
おうぎ形の中心角②(半径のみ)
ログイン
半径 12cm、弧の長さ 3πcmのおうぎ形の中心角は何°ですか?
いろいろな立体(5)
1-6-1-1
柱・錐
ログイン
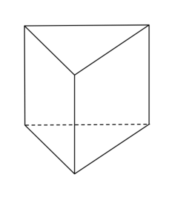
この立体の名前は何ですか?
1-6-1-2
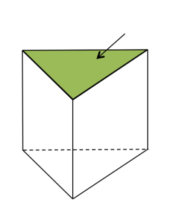
立体の部分の名前
ログイン
→の部分の名称を答えましょう。
1-6-1-3
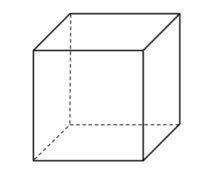
多面体
ログイン
この多面体の名前は何でしょうか?
1-6-1-4
展開図
ログイン
次の展開図を組み立ててできる
立体の名前(柱・錐)を答えましょう。
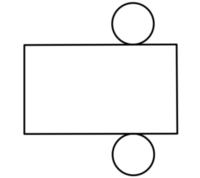
1-6-1-5
混合問題
ログイン
この立体の名前は何ですか?

空間内の平面と直線(4)
1-6-2-1
2直線の位置関係
ログイン
この直方体(ティッシュボックス)について
辺ABと交わっている辺はどれでしょうか?(すべて)
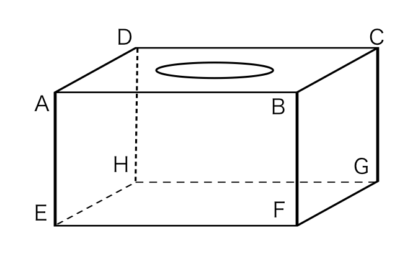
1-6-2-2
直線と面の位置関係
ログイン
この直方体(ティッシュボックス)について
面ABCDと垂直な辺はどれでしょうか?(すべて)

1-6-2-3
2平面の位置関係
ログイン
この直方体(ティッシュボックス)について
面ABCDと垂直な面はどれでしょうか?(すべて)

1-6-2-4
混合問題
ログイン
この直方体(ティッシュボックス)について
辺ABとねじれの辺はどれでしょうか?(すべて)

動かしてできる立体(3)
1-6-3-1
回転・線を動かして出来る立体
ログイン
これから ℓ のまわりに長方形を一回転させます。
こうした時の→の ℓ の名前は何でしょうか?
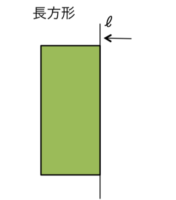
1-6-3-2
回転体を描けるかの確認問題
ログイン
この図を、直線 ℓ を軸として1回転して出来る回転体の
見取り図を描けますか?(点数はつきません)
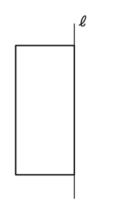
1-6-3-3
投影図
ログイン
図のように立体を真正面(横)から見た図を何と言いますか?
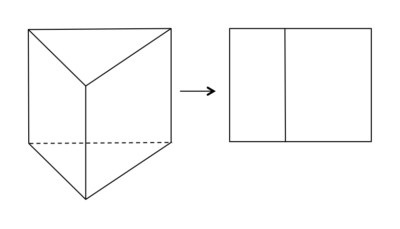
立体の体積と表面積(6)
1-6-4-1
柱の体積・表面積
ログイン
この立体の「体積」を求めましょう。
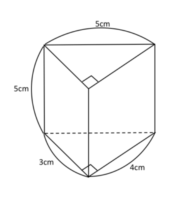
1-6-4-2
円錐の側面積・おうぎ形の面積
ログイン
中心角が分からない時、
おうぎ型の面積を求める公式は何でしょうか?
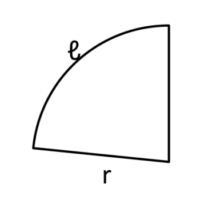
1-6-4-3
錐の体積・表面積
ログイン
この立体の「体積」を求めましょう。
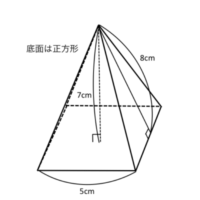
1-6-4-4
体積・表面積のまとめ
ログイン
底面積が 32cm² 、高さが 6cm の三角柱の体積はいくつですか?
1-6-4-5
球の体積・表面積
ログイン
この球の体積は?
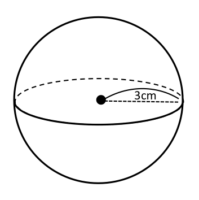
1-6-4-6
混合問題
ログイン
この立体の「体積」を求めましょう。

資料の活用(8)
1-7-1-1
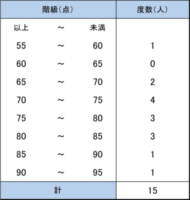
度数分布表
ログイン
この表はクラスの社会の点数ををまとめたものである。
このような表を何といいますか?
1-7-1-2
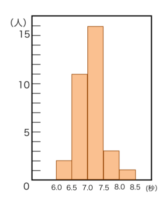
ヒストグラム
ログイン
度数分布表をもとにあらわしたこのようなグラフを何といいますか?
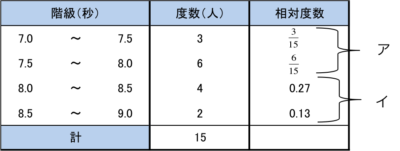
1-7-1-3
相対度数
ログイン
正しいのはどっち?
1-7-1-5
平均値・最頻値・中央値
ログイン
資料の値を大きさの順に並べたとき、中央の値をなんといいますか?
1-7-1-5
累積度数・累積相対度数
ログイン
度数分布表において、小さい方からある階級までの度数の総和をその階級の何といいますか?
1-7-1-6
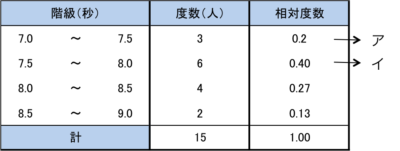
度数分布表と階級値・平均値
ログイン
この表の階級値のアを求めましょう。

1-7-1-8
統計的確率
ログイン
1-7-1-9
混合問題
ログイン
正しいのはどっち?