先生ページ

数学

★
●
●
2025.12.13
キーボードを使って解く方法(1)
  • 0-0-0-0
    キーボードを使って解く方法

    この問題は、答えを自分で入力する問題です。
    解答欄に「さいたま」と入力してみましょう。

    入力が終わったら、「Enterキー（エンターキー）」を押しましょう。
    「Enterキー」を押すと、次の問題に進みます。

    keyboard_Enter

    • 数と式(36)
  • 4-1-1-1
    言葉ときまり
    単項式の数の部分を何といいますか？
  • 4-1-1-2
    単項式の係数と次数
    次の単項式の係数と次数は何ですか？

    -3x³y²z

  • 4-1-1-3
    多項式の係数と次数・降べきの順
    次の整式は何次式ですか？

    4x³-2x²-3x³+6+x

  • 4-1-2-1
    多項式の加法・減法

    (x²+3x-3)+(3x²-x-4)=?

  • 4-1-2-2
    代入の式 A=x²+3x-3
    A=x²+3x-3  B=x²+2x-2 のとき次の式を計算しましょう。

    A-2B

  • 4-1-3-1
    単項式の乗法

    2x²y×(-3x²y²)=?

  • 4-1-3-2
    分配法則

    2xy(-3x²+3x-2y)=?

  • 4-1-4-1
    中学の展開

    (x-3y)(x-3y)=?

  • 4-1-4-2
    因数分解の公式（a³+b³）

    新しい公式の確認問題

  • 4-1-4-3
    新しい公式を使った展開（a³+b³）

    (2a+3b)³=?

  • 4-1-4-4
    おきかえによる展開

    (x²+2x-3)(x²+2x+4)=?

  • 4-1-5-1
    中学の復習
    因数分解しましょう。
    x²-3xy-10y²
  • 4-1-5-2
    たすきがけ
    因数分解しましょう。

    2x²+7xy+3y²

  • 4-1-5-3
    たすきがけが苦手な人向け
    たすきがけ以外の方法の手順について一緒にやっていきましょう！
    ＜手順1＞

    1

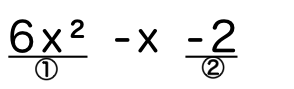
    ①の係数を②にかけましょう。
  • 4-1-5-4
    ３乗の式
    因数分解しましょう。

    x³+8

  • 4-1-5-5
    おきかえを使った因数分解
    因数分解しましょう。

    (x+2y)²+5(x+2y)+6

  • 4-1-5-6
    次数の低い文字について整理
    因数分解しましょう。

    xy-x-y+1

  • 4-1-5-7
    式のたすきがけ①
    因数分解しましょう。

    x²+(5y+1)x+(2y-1)(3y+2)

  • 4-1-5-8
    式のたすきがけ②
    因数分解しましょう。

    x²+3xy+2y²+2x+3y+1

  • 4-1-6-1
    絶対値
    次の値を求めましょう。

    |3|

  • 4-1-6-2
    絶対値記号の外し方
    次の式を絶対値の記号を用いずに表しましょう。

    |a-4|

  • 4-1-7-1
    中学の復習

    2√12-3√48+√24=?

  • 4-1-7-2
    分母の有理化

    4-1-7-2

  • 4-1-7-3
    対称式などの知識
    x+y,x²+y² のように x と y を入れ替えても変わらない式を、x, y の何といいますか？
  • 4-1-7-4
    対称式

    4-1-7-4

  • 4-2-1-1
    一次不等式
    次の不等式を解きましょう。

    x-6<3x+4

    ※どちらかに x が入ります。
  • 4-2-1-2
    不等式のとりうる範囲
    3 < x < 7 である x について
    次の式のとりうる範囲を求めましょう。 

    x-4

  • 4-2-1-3
    連立不等式
    次の連立不等式を満たす x の範囲を求めましょう。

    3x-4 < x+10

    2x+1 ≦ 3x+7

  • 4-2-1-4
    不等式の応用問題
    Aさんの通う学校から自宅までの道のりは 20km です。
    この道のりを初めは時速 4km,
    途中から時速3kmで歩いたら所要時間は 6時間以内 でした。
    時速 4km で歩いた道のりは何km以上ですか？
  • 4-2-1-5
    絶対値を含む方程式・不等式
    次の方程式、不等式を解きましょう。

    |2-x|=5

  • 4-2-2-1
    ２次方程式（中学内容）
    次の２次方程式を解きましょう。
    x²=18
  • 4-2-2-2
    ２次方程式の解の個数
    次の２次方程式の実数解の個数を調べましょう。

    3x²-x+1=0

  • 4-2-2-3
    ２次方程式が実数解を持つ条件
    次の x についての２次方程式が重解をもつように定数 k の値を求めましょう。

    2x²+kx+k+1=0

  • 4-2-2-4
    連立２元２次方程式と連立３元１次方程式
    次の連立方程式を解きましょう。

    x+3y=1

    2x²+y²=9

  • 4-2-2-5
    解から方程式を決定する・共通解の問題

    4-2-2-5

  • 4-2-2-6
    ２次方程式の文章問題
    直角をはさむ２辺の和が17cmで、
    斜辺の長さが13cmの直角三角形があります。
    このとき底辺と高さを求めましょう。（底辺の長さは高さより長い）
    • 集合と論証(12)
  • 4-3-1-1
    集合と要素
    「１から２０までの奇数の集まり」、などのように
    範囲がはっきりしたものの集まりを何といいますか？
  • 4-3-1-2
    部分集合
    次の２つの集合の関係を表す記号を選びましょう。

    A={1,2,3,4,…,10}, B={1,4,9}

  • 4-3-1-3
    共通部分と和集合
    矢印（↓）の部分を何といいますか？

    1

     

  • 4-3-1-4
    補集合
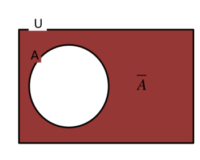
    全体集合をU,その部分集合をAとするとき、
    Uの要素であって
    Aの要素でないものをを何といいますか？

    1-133-e1493007537786

  • 4-3-1-5
    補集合②
    1から12までの自然数の集合を全体集合Uとし、
    その中で8の約数の集合をA,
    12の約数をBとするとき、次の集合の要素を入力しましょう。

    A∩B

  • 4-3-1-6
    文章問題
    ある中学生100人に数学が「好きか、好きではないか？」と
    「得意か、得意でないか」についてアンケートをとった。
    好きと答えた中学生は 35人、
    得意と答えた中学生は 25人、
    好きでも得意でもない中学生は 48人いました。
    この時、「数学が好きまたは、得意である」と答えた中学生は何人ですか？ 
  • 4-3-2-1
    命題（真偽）
    次の命題の真偽を選びましょう。
    y=0ならばxy=0
  • 4-3-2-2
    必要条件・十分条件
    空欄に入るのはどれですか？
    a=2 かつ b=6　は　ab=12であるための　　　　　条件である。
  • 4-3-2-3
    条件・命題の否定
    次の条件の否定を述べたものはどれでしょうか？
    x > 2 
  • 4-3-2-4
    逆・裏・対偶
    命題 p ⇒ qに対して
    q ⇒ p を何と言いますか？
  • 4-3-2-5
    対偶を利用した証明
    整数xの平方が偶数ならば、x は偶数であることを証明していきます。
    下線部の部分に当てはまる式や言葉を選びましょう。
    この命題の対偶「　　　　　　　　」を証明する。
  • 4-3-2-6
    背理法を利用した証明
    ある命題を証明する時、
    「その命題が成り立たないと仮定すると矛盾が生じる。
    したがってその命題は成り立つ」
    と主張するような証明法をなんといいますか？
    • ２次関数（高校）(14)
  • 4-4-1-1
    関数f (x) の値
    関数 f(x)=x²+x において次の値を求めましょう。
     f(-2)
  • 4-4-1-2
    軸と頂点
    次の２次関数の軸と頂点を求めましょう。
    y=x²
  • 4-4-1-3
    平方完成の手順
    y=ax²+bx+c を y=a(x-p)²+q の形に変形することを何と言いますか？
  • 4-4-1-4
    平方完成
    次のy=ax²+bx+c の式を
    y=a(x-p)²+q の形に変形（平方完成）させましょう。
    y=x²-6x+2
  • 4-4-1-5
    グラフを選ぶ
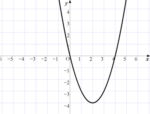
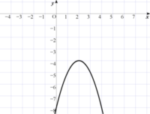
    y=(x-2)²-4のグラフはどれですか？

    x-2^2-4-1-e1493977710544

    x-2^2-4-e1493975133606

  • 4-4-1-6
    関数の最大値・最小値
    x がとる値の範囲のことを何と言いますか？
  • 4-4-2-1
    2次関数のグラフと x 軸との共有点
    次の2次関数のグラフの共有点の個数を求めましょう。(0,1,2を入力）
    また共有点がある場合はそのx座標を入力しましょう。（ない場合は空欄）
    y=2x²-3x+4
  • 4-4-2-2
    2次不等式
    次の２次不等式を解きましょう
    x²-2x-3<0
  • 4-4-2-3
    連立2次不等式
    次の連立２次不等式を解きましょう。
    x²+7x+10<0
    x²+3x-4<0

     

  • 4-4-2-4
    2次関数の決定
    頂点が (2, -3) で、点 (4, -7) を通る２次関数を求めましょう。
                                  ※ y=a(x-p)²+qの形で入力してください。
  • 4-4-2-5
    グラフの平行移動
    点 (a, b) を x 軸方向に p, y 軸方向に q 移動したときの座標はどうなりますか？
    空欄を埋めましょう。
  • 4-4-2-6
    グラフの対称移動
    放物線 y=x²-2x+5 を
    x軸に関して対称移動した2次関数を求めましょう。
       ※y=ax²+bx+cの形で入力してください。
  • 4-4-2-7
    放物線の位置関係
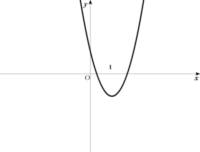
    2次関数 y=ax²+bx+c のグラフが
    下の図のようになるとき、
    aの符号はどちらですか？

    1-134-e1494837759897

  • 4-4-2-8
    最大・最小による式の決定
    y=x²+x+c (-1 ≦ x ≦ 1)の最大値が 5 のとき
    定数 c を求めましょう。
    • 図形と計量(17)
  • 4-5-1-1
    三角比の用語
    【位置・名称の確認】
    (∠)Aの対辺を何と呼びますか？

    1

  • 4-5-1-2
    特別な三角比
    sin30°=
  • 4-5-1-3
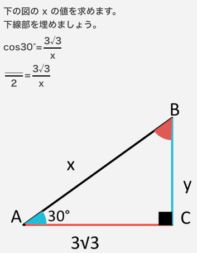
    長さを求める手順

    4-5-1-3

  • 4-5-1-4
    三角比の相互関係①（公式を覚える）
    sin30°=?
  • 4-5-1-5
    三角比の相互関係②（どの公式を使うか）
    sinθだけ分かっている時
    cosθを求める時に使う公式を選びましょう。
  • 4-5-1-6
    相互関係/実践問題①（θ<90°）

    4-5-1-6

  • 4-5-2-1
    90°-θの三角比
    1,sin(90°-θ)  2,cos(90°-θ) 3,tan(90°-θ)
  • 4-5-2-2
    三角比の拡張①（180°-θ,90°+θの確認）
    0 ≦ θ ≦ 180
    sin(180°-θ)=?
  • 4-5-2-3
    三角比の拡張②（鈍角の三角比）
    150°の正弦の値を求めましょう。
    ※左の空欄に+,-の符号を入力してください。
  • 4-5-2-4
    三角比の拡張③（三角比の式をまとめる）
    次の式の値を求めましょう。
    tan(180°-θ)tan(90°-θ)
  • 4-5-2-5
    三角方程式

    4-5-2-5

  • 4-5-2-6
    相互関係/実践問題②（0°≦θ≦180°）

    4-5-2-6

  • 4-5-3-1
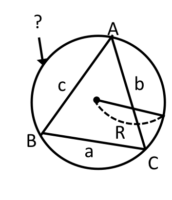
    正弦定理
    三角形ABCの外側の円を何と言いますか？

    2-130

  • 4-5-3-2
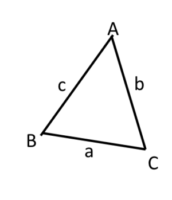
    余弦定理
    余弦定理の公式を表した下の図の下線部を埋めましょう。
    a²=b²+c²-2     cosA

    3-124-e1496046485941

  • 4-5-3-3
    正弦・余弦定理の混合問題
    三角形の残りの辺や角を求める問題で
    「3つの辺」が分かる時に使う定理はどちらですか？
  • 4-5-3-4
    三角形の面積①（公式にあてはめて解く）
    下の図の三角形でcを底辺とした時、
    高さを表すものをすべて選びましょう。

    4-112

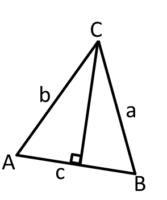
  • 4-5-3-5
    三角形の面積②（３辺から解く手順）
    次のような△ABCの面積を求めます。
    下線部を埋めてください。
    a=6, b=9, c=5
    ３辺がわかるので         を使う。

     

    • データの分析(7)
  • 2-7-1-1
    四分位数
    下のデータはあるゲームをした時のAさんの得点です。
    最小値と最大値を求めましょう。
    （点）

    2-132

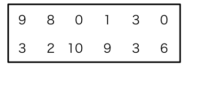
  • 2-7-1-2
    箱ひげ図

    4-6-1-4

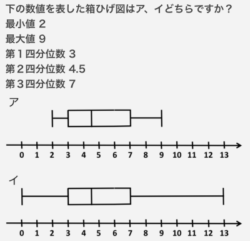
  • 4-6-1-1
    データの用語
    この表はあるサッカークラブのメンバー33人の
    50m走のタイムをまとめたものである。
    このような表を何といいますか？

    50m-e1481802997193

  • 4-6-1-2
    代表値

    この表は、あるソフトボール部15名の
    ソフトボール投げの記録をまとめたものです。

    平均値はいくつですか？

    1-89-e1481893252170

  • 4-6-2-1
    分散と散布図の用語
    （データの個々の値）-（平均値）を何と言いますか？
  • 4-6-2-2
    分散と標準偏差を求める手順
    この表はAとBの２人のゲームの点数です。
    どちらの方が点数に散らばりがあるか調べたいです。

    1-142

     

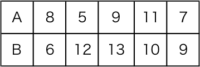
  • 4-6-2-3
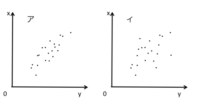
    相関図
    相関が強いのはどちらですか？

    1.1-17-e1496396384771

    • 係数と次数(3)
  • 4-1-1-1
    言葉ときまり
    単項式の数の部分を何といいますか？
  • 4-1-1-2
    単項式の係数と次数
    次の単項式の係数と次数は何ですか？

    -3x³y²z

  • 4-1-1-3
    多項式の係数と次数・降べきの順
    次の整式は何次式ですか？

    4x³-2x²-3x³+6+x

    • 多項式の加減(2)
  • 4-1-2-1
    多項式の加法・減法

    (x²+3x-3)+(3x²-x-4)=?

  • 4-1-2-2
    代入の式 A=x²+3x-3
    A=x²+3x-3  B=x²+2x-2 のとき次の式を計算しましょう。

    A-2B

    • 整式の乗法(2)
  • 4-1-3-1
    単項式の乗法

    2x²y×(-3x²y²)=?

  • 4-1-3-2
    分配法則

    2xy(-3x²+3x-2y)=?

    • 新しい公式を使った展開(4)
  • 4-1-4-1
    中学の展開

    (x-3y)(x-3y)=?

  • 4-1-4-2
    因数分解の公式（a³+b³）

    新しい公式の確認問題

  • 4-1-4-3
    新しい公式を使った展開（a³+b³）

    (2a+3b)³=?

  • 4-1-4-4
    おきかえによる展開

    (x²+2x-3)(x²+2x+4)=?

    • 因数分解(8)
  • 4-1-5-1
    中学の復習
    因数分解しましょう。
    x²-3xy-10y²
  • 4-1-5-2
    たすきがけ
    因数分解しましょう。

    2x²+7xy+3y²

  • 4-1-5-3
    たすきがけが苦手な人向け
    たすきがけ以外の方法の手順について一緒にやっていきましょう！
    ＜手順1＞

    1

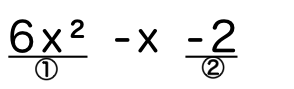
    ①の係数を②にかけましょう。
  • 4-1-5-4
    ３乗の式
    因数分解しましょう。

    x³+8

  • 4-1-5-5
    おきかえを使った因数分解
    因数分解しましょう。

    (x+2y)²+5(x+2y)+6

  • 4-1-5-6
    次数の低い文字について整理
    因数分解しましょう。

    xy-x-y+1

  • 4-1-5-7
    式のたすきがけ①
    因数分解しましょう。

    x²+(5y+1)x+(2y-1)(3y+2)

  • 4-1-5-8
    式のたすきがけ②
    因数分解しましょう。

    x²+3xy+2y²+2x+3y+1

    • 絶対値(2)
  • 4-1-6-1
    絶対値
    次の値を求めましょう。

    |3|

  • 4-1-6-2
    絶対値記号の外し方
    次の式を絶対値の記号を用いずに表しましょう。

    |a-4|

    • 平方根（高Ⅰ）(4)
  • 4-1-7-1
    中学の復習

    2√12-3√48+√24=?

  • 4-1-7-2
    分母の有理化

    4-1-7-2

  • 4-1-7-3
    対称式などの知識
    x+y,x²+y² のように x と y を入れ替えても変わらない式を、x, y の何といいますか？
  • 4-1-7-4
    対称式

    4-1-7-4

    • 不等式(5)
  • 4-2-1-1
    一次不等式
    次の不等式を解きましょう。

    x-6<3x+4

    ※どちらかに x が入ります。
  • 4-2-1-2
    不等式のとりうる範囲
    3 < x < 7 である x について
    次の式のとりうる範囲を求めましょう。 

    x-4

  • 4-2-1-3
    連立不等式
    次の連立不等式を満たす x の範囲を求めましょう。

    3x-4 < x+10

    2x+1 ≦ 3x+7

  • 4-2-1-4
    不等式の応用問題
    Aさんの通う学校から自宅までの道のりは 20km です。
    この道のりを初めは時速 4km,
    途中から時速3kmで歩いたら所要時間は 6時間以内 でした。
    時速 4km で歩いた道のりは何km以上ですか？
  • 4-2-1-5
    絶対値を含む方程式・不等式
    次の方程式、不等式を解きましょう。

    |2-x|=5

    • ２次方程式(6)
  • 4-2-2-1
    ２次方程式（中学内容）
    次の２次方程式を解きましょう。
    x²=18
  • 4-2-2-2
    ２次方程式の解の個数
    次の２次方程式の実数解の個数を調べましょう。

    3x²-x+1=0

  • 4-2-2-3
    ２次方程式が実数解を持つ条件
    次の x についての２次方程式が重解をもつように定数 k の値を求めましょう。

    2x²+kx+k+1=0

  • 4-2-2-4
    連立２元２次方程式と連立３元１次方程式
    次の連立方程式を解きましょう。

    x+3y=1

    2x²+y²=9

  • 4-2-2-5
    解から方程式を決定する・共通解の問題

    4-2-2-5

  • 4-2-2-6
    ２次方程式の文章問題
    直角をはさむ２辺の和が17cmで、
    斜辺の長さが13cmの直角三角形があります。
    このとき底辺と高さを求めましょう。（底辺の長さは高さより長い）
    • 集合の表し方(6)
  • 4-3-1-1
    集合と要素
    「１から２０までの奇数の集まり」、などのように
    範囲がはっきりしたものの集まりを何といいますか？
  • 4-3-1-2
    部分集合
    次の２つの集合の関係を表す記号を選びましょう。

    A={1,2,3,4,…,10}, B={1,4,9}

  • 4-3-1-3
    共通部分と和集合
    矢印（↓）の部分を何といいますか？

    1

     

  • 4-3-1-4
    補集合
    全体集合をU,その部分集合をAとするとき、
    Uの要素であって
    Aの要素でないものをを何といいますか？

    1-133-e1493007537786

  • 4-3-1-5
    補集合②
    1から12までの自然数の集合を全体集合Uとし、
    その中で8の約数の集合をA,
    12の約数をBとするとき、次の集合の要素を入力しましょう。

    A∩B

  • 4-3-1-6
    文章問題
    ある中学生100人に数学が「好きか、好きではないか？」と
    「得意か、得意でないか」についてアンケートをとった。
    好きと答えた中学生は 35人、
    得意と答えた中学生は 25人、
    好きでも得意でもない中学生は 48人いました。
    この時、「数学が好きまたは、得意である」と答えた中学生は何人ですか？ 
    • 論証(6)
  • 4-3-2-1
    命題（真偽）
    次の命題の真偽を選びましょう。
    y=0ならばxy=0
  • 4-3-2-2
    必要条件・十分条件
    空欄に入るのはどれですか？
    a=2 かつ b=6　は　ab=12であるための　　　　　条件である。
  • 4-3-2-3
    条件・命題の否定
    次の条件の否定を述べたものはどれでしょうか？
    x > 2 
  • 4-3-2-4
    逆・裏・対偶
    命題 p ⇒ qに対して
    q ⇒ p を何と言いますか？
  • 4-3-2-5
    対偶を利用した証明
    整数xの平方が偶数ならば、x は偶数であることを証明していきます。
    下線部の部分に当てはまる式や言葉を選びましょう。
    この命題の対偶「　　　　　　　　」を証明する。
  • 4-3-2-6
    背理法を利用した証明
    ある命題を証明する時、
    「その命題が成り立たないと仮定すると矛盾が生じる。
    したがってその命題は成り立つ」
    と主張するような証明法をなんといいますか？
    • ２次関数のグラフ(6)
  • 4-4-1-1
    関数f (x) の値
    関数 f(x)=x²+x において次の値を求めましょう。
     f(-2)
  • 4-4-1-2
    軸と頂点
    次の２次関数の軸と頂点を求めましょう。
    y=x²
  • 4-4-1-3
    平方完成の手順
    y=ax²+bx+c を y=a(x-p)²+q の形に変形することを何と言いますか？
  • 4-4-1-4
    平方完成
    次のy=ax²+bx+c の式を
    y=a(x-p)²+q の形に変形（平方完成）させましょう。
    y=x²-6x+2
  • 4-4-1-5
    グラフを選ぶ
    y=(x-2)²-4のグラフはどれですか？

    x-2^2-4-1-e1493977710544

    x-2^2-4-e1493975133606

  • 4-4-1-6
    関数の最大値・最小値
    x がとる値の範囲のことを何と言いますか？
    • ２次関数の応用(8)
  • 4-4-2-1
    2次関数のグラフと x 軸との共有点
    次の2次関数のグラフの共有点の個数を求めましょう。(0,1,2を入力）
    また共有点がある場合はそのx座標を入力しましょう。（ない場合は空欄）
    y=2x²-3x+4
  • 4-4-2-2
    2次不等式
    次の２次不等式を解きましょう
    x²-2x-3<0
  • 4-4-2-3
    連立2次不等式
    次の連立２次不等式を解きましょう。
    x²+7x+10<0
    x²+3x-4<0

     

  • 4-4-2-4
    2次関数の決定
    頂点が (2, -3) で、点 (4, -7) を通る２次関数を求めましょう。
                                  ※ y=a(x-p)²+qの形で入力してください。
  • 4-4-2-5
    グラフの平行移動
    点 (a, b) を x 軸方向に p, y 軸方向に q 移動したときの座標はどうなりますか？
    空欄を埋めましょう。
  • 4-4-2-6
    グラフの対称移動
    放物線 y=x²-2x+5 を
    x軸に関して対称移動した2次関数を求めましょう。
       ※y=ax²+bx+cの形で入力してください。
  • 4-4-2-7
    放物線の位置関係
    2次関数 y=ax²+bx+c のグラフが
    下の図のようになるとき、
    aの符号はどちらですか？

    1-134-e1494837759897

  • 4-4-2-8
    最大・最小による式の決定
    y=x²+x+c (-1 ≦ x ≦ 1)の最大値が 5 のとき
    定数 c を求めましょう。
    • 三角比(6)
  • 4-5-1-1
    三角比の用語
    【位置・名称の確認】
    (∠)Aの対辺を何と呼びますか？

    1

  • 4-5-1-2
    特別な三角比
    sin30°=
  • 4-5-1-3
    長さを求める手順

    4-5-1-3

  • 4-5-1-4
    三角比の相互関係①（公式を覚える）
    sin30°=?
  • 4-5-1-5
    三角比の相互関係②（どの公式を使うか）
    sinθだけ分かっている時
    cosθを求める時に使う公式を選びましょう。
  • 4-5-1-6
    相互関係/実践問題①（θ<90°）

    4-5-1-6

    • 三角比の応用(6)
  • 4-5-2-1
    90°-θの三角比
    1,sin(90°-θ)  2,cos(90°-θ) 3,tan(90°-θ)
  • 4-5-2-2
    三角比の拡張①（180°-θ,90°+θの確認）
    0 ≦ θ ≦ 180
    sin(180°-θ)=?
  • 4-5-2-3
    三角比の拡張②（鈍角の三角比）
    150°の正弦の値を求めましょう。
    ※左の空欄に+,-の符号を入力してください。
  • 4-5-2-4
    三角比の拡張③（三角比の式をまとめる）
    次の式の値を求めましょう。
    tan(180°-θ)tan(90°-θ)
  • 4-5-2-5
    三角方程式

    4-5-2-5

  • 4-5-2-6
    相互関係/実践問題②（0°≦θ≦180°）

    4-5-2-6

    • 正弦定理・余弦定理(5)
  • 4-5-3-1
    正弦定理
    三角形ABCの外側の円を何と言いますか？

    2-130

  • 4-5-3-2
    余弦定理
    余弦定理の公式を表した下の図の下線部を埋めましょう。
    a²=b²+c²-2     cosA

    3-124-e1496046485941

  • 4-5-3-3
    正弦・余弦定理の混合問題
    三角形の残りの辺や角を求める問題で
    「3つの辺」が分かる時に使う定理はどちらですか？
  • 4-5-3-4
    三角形の面積①（公式にあてはめて解く）
    下の図の三角形でcを底辺とした時、
    高さを表すものをすべて選びましょう。

    4-112

  • 4-5-3-5
    三角形の面積②（３辺から解く手順）
    次のような△ABCの面積を求めます。
    下線部を埋めてください。
    a=6, b=9, c=5
    ３辺がわかるので         を使う。

     

    • データの分析１(7)
  • 2-7-1-1
    四分位数
    下のデータはあるゲームをした時のAさんの得点です。
    最小値と最大値を求めましょう。
    （点）

    2-132

  • 2-7-1-2
    箱ひげ図

    4-6-1-4

  • 4-6-1-1
    データの用語
    この表はあるサッカークラブのメンバー33人の
    50m走のタイムをまとめたものである。
    このような表を何といいますか？

    50m-e1481802997193

  • 4-6-1-2
    代表値

    この表は、あるソフトボール部15名の
    ソフトボール投げの記録をまとめたものです。

    平均値はいくつですか？

    1-89-e1481893252170

  • 4-6-2-1
    分散と散布図の用語
    （データの個々の値）-（平均値）を何と言いますか？
  • 4-6-2-2
    分散と標準偏差を求める手順
    この表はAとBの２人のゲームの点数です。
    どちらの方が点数に散らばりがあるか調べたいです。

    1-142

     

  • 4-6-2-3
    相関図
    相関が強いのはどちらですか？

    1.1-17-e1496396384771

    • 総問題数：2663