4-5-3-1 正弦定理
三角形ABCの外側の円を何と言いますか?
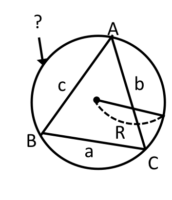
問題 1
三角形ABCの外側の円を何と言いますか?
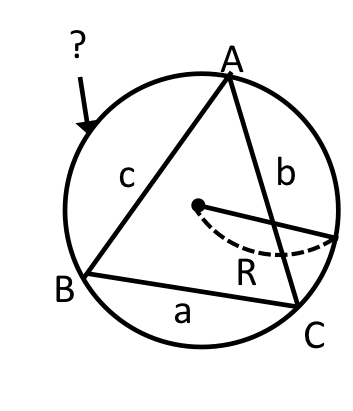
正解 :外接円
問題 2
正弦定理の公式です。
下線部を埋めましょう。
asin = sinB=csinC=2
sin
sinB
sinC
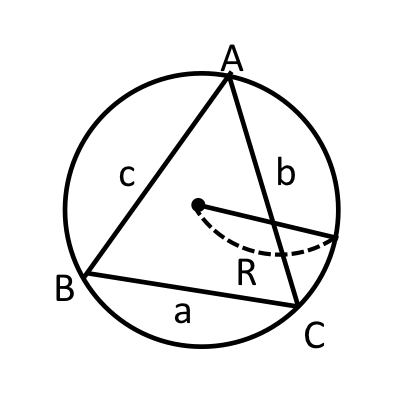
正解 :A,b,R
問題 3△ABCにおいて、b=3√2, a=3, B=45°のとき
△ABCにおいて、b=3√2, a=3, B=45°のとき
Aおよび外接円の半径Rを求めましょう。
正解 :30,3
問題 4△ABCにおいて、C=30°, R=2 のとき
△ABCにおいて、C=30°, R=2 のとき
cを求めましょう。
正解 :2
問題 5△ABCにおいて、a=2√3, A=120°, B=30°のとき
△ABCにおいて、a=2√3, A=120°, B=30°のとき
cおよび外接円の半径Rを求めましょう。
正解 :2,2
問題 6△ABCにおいて、a=4, A=30°, C=105°のとき
△ABCにおいて、a=4, A=30°, C=105°のとき
bおよび外接円の半径Rを求めましょう。
正解 :4,2,4
問題 7△ABCにおいて、a=√6, c=2, A=60°のとき
△ABCにおいて、a=√6, c=2, A=60°のとき
BおよびCを求めましょう。
正解 :75,45
問題 8△ABCにおいて、A=60°, a=3, B=45°のとき
△ABCにおいて、A=60°, a=3, B=45°のとき
bおよび外接円の半径Rを求めましょう。
正解 :6,3
問題 9△ABCにおいて、c=√2, R=1, B=50°のとき
△ABCにおいて、c=√2, R=1, B=50°のとき
AおよびCを求めましょう。
正解 :85,45
問題 10△ABCにおいて、A=45°, b=10√6, B=60°のとき
△ABCにおいて、A=45°, b=10√6, B=60°のとき
aおよび外接円の半径Rを求めましょう。
正解 :20,10,2
問題 11△ABCにおいて、a=10√2, b=10, A=135°のとき
△ABCにおいて、a=10√2, b=10, A=135°のとき
Bを求めましょう。
正解 :30
問題 12△ABCにおいて、A=120°, B=15°, c=3√2のとき
△ABCにおいて、A=120°, B=15°, c=3√2のとき
aおよびCを求めましょう。
正解 :3,3,45
問題 13△ABCにおいて、a=15, B=60°, C=75°のとき
△ABCにおいて、a=15, B=60°, C=75°のとき
bおよび外接円の半径Rを求めましょう。
正解 :15,6,2,15,2,2
問題 14△ABCにおいて、c=12, B=135°, 外接円の半径R=12のとき
△ABCにおいて、c=12, B=135°, 外接円の半径R=12のとき
bおよびCを求めましょう。
正解 :12,2,30
問題 15△ABCにおいて、b=√3, c=√2, C=45°のとき
△ABCにおいて、b=√3, c=√2, C=45°のとき
Bを求めましょう。
正解 :60,120
問題 16△ABCにおいて、R=5, B=60°のとき
△ABCにおいて、R=5, B=60°のとき
bを求めましょう。
正解 :5,3