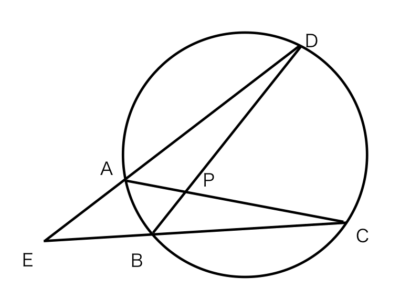
3-6-4-1 円周角の定理を使った相似の証明
△APB ∽ △DPCであることを証明しましょう。
△APB と △DPCにおいて
弧?に対する円周角なので∠PAB=∠PDC・・・①
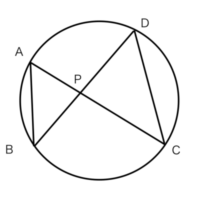
問題 1△APB と △DPCにおいて
△APB ∽ △DPCであることを証明しましょう。
△APB と △DPCにおいて
弧?に対する円周角なので∠PAB=∠PDC・・・①
正解 :BC
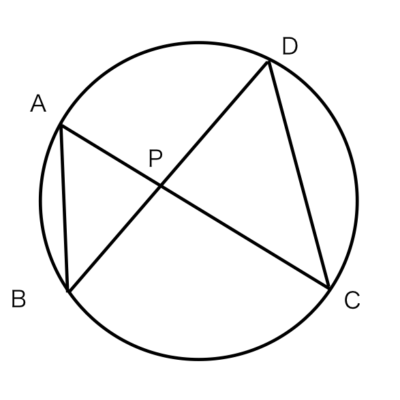
問題 2△APB と △DPCにおいて
△APB ∽ △DPCであることを証明しましょう。
△APB と △DPCにおいて
弧BCに対する円周角なので∠PAB=∠PDC・・・①
弧?に対する円周角なので∠PBA=∠PCD・・・②

正解 :DA
問題 3△APB ∽ △DPCであることを証明しましょう。
△APB と △DPCにおいて
△APB ∽ △DPCであることを証明しましょう。
△APB と △DPCにおいて
弧BCに対する円周角なので∠PAB=∠PDC・・・①
弧DAに対する円周角なので∠PBA=∠PCD・・・②
①、②より?ので
△APB ∽ △DPC

正解 :2組の角がそれぞれ等しい
問題 4弧BC=弧CDのとき
△ABC と △BPCにおいて
弧BC=弧CDのとき
△ABC ∽ △BPCであることを証明しましょう。
△ABC と △BPCにおいて
?なので∠ACB=∠BCP・・・①
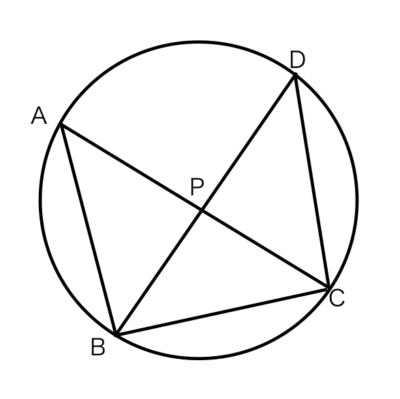
正解 :共通
問題 5弧BC=弧CDのとき
△ABC と △BPCにおいて
弧BC=弧CDのとき
△ABC ∽ △BPCであることを証明しましょう。
△ABC と △BPCにおいて
共通なので∠ACB=∠BCP・・・①
仮定より弧BC=弧CD
等しい弧に対する円周角は等しいので
∠BAC=∠?・・・②

正解 :PBC
問題 6弧BC=弧CDのとき
△ABC と △BPCにおいて
弧BC=弧CDのとき
△ABC ∽ △BPCであることを証明しましょう。
△ABC と △BPCにおいて
共通なので∠ACB=∠BCP・・・①
仮定より弧BC=弧CD
等しい弧に対する円周角は等しいので
∠BAC=∠PBC・・・②
①、②より?なので
△ABC ∽ △BPC

正解 :2組の角がそれぞれ等しい
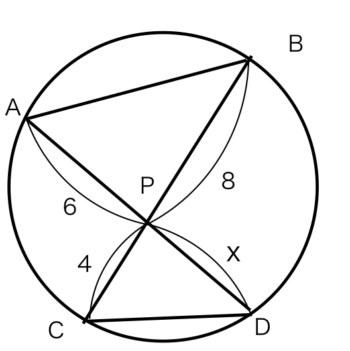
問題 7x=?
x=?
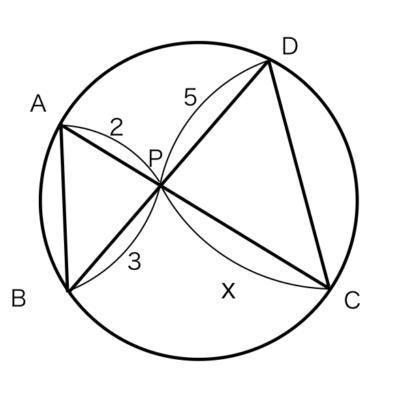
正解 :15,2
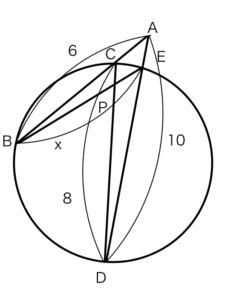
問題 8△AEC と △BEDにおいて
△AEC ∽ △BEDを証明しましょう。
△AEC と △BEDにおいて
弧ABに対する円周角は等しいので
∠ACE=∠?・・・①
正解 :BDE
問題 9△AEC と △BEDにおいて
△AEC ∽ △BEDを証明しましょう。
△AEC と △BEDにおいて
弧ABに対する円周角は等しいので
∠ACE=∠BDE・・・①
?なので∠AEC=∠BED・・・②

正解 :共通
問題 10△AEC と △BEDにおいて
△AEC ∽ △BEDを証明しましょう。
△AEC と △BEDにおいて
弧ABに対する円周角は等しいので
∠ACE=∠BDE・・・①
共通なので∠AEC=∠BED・・・②
①、②より?なので
△AEC ∽ △BED

正解 :2組の角がそれぞれ等しい
問題 11
x=?
正解 :16,3
問題 12
x=?
正解 :24,5