2-5-3-4 性質を利用した証明②
この図の△ABCと△CDEは正三角形です。
線分AD、線分BEを引くとき
△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCDにおいて
△ABCと△CDEは正三角形なので
AC=?・・・①
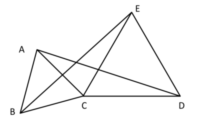
この図の△ABCと△CDEは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCDにおいて
△ABCと△CDEは正三角形なので
AC=?・・・①
正解 :BC
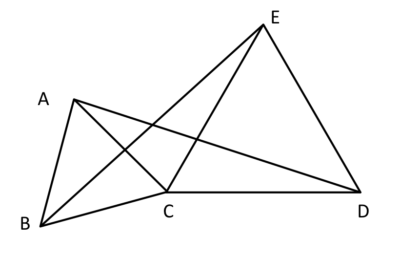
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=?・・・②

正解 :CE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠?+∠ECD

正解 :ACE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠?+60°

正解 :ACE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠ACE+60°
∠BCE=∠ACB+∠ACE
=60°+∠ACE
よって
∠ACD=∠?・・・③

正解 :BCE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くとき△ACD≡△BCEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ECD+∠ACE
=60°+∠ACE
∠BCE=∠ACB+∠ACE
=60°+∠ACE
よって
∠ACD=∠BCE・・・③
①、②、③より?ので
△ACD≡△BCE

正解 :2組の辺とその間の角がそれぞれ等しい。 (SAS)
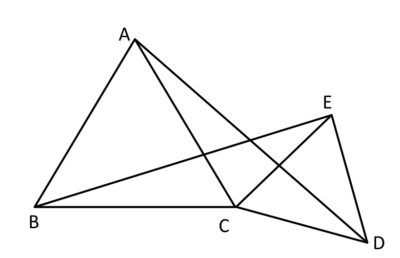
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCDにおいて
△ABCと△CDEは正三角形なので
?=BC・・・①
正解 :AC
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
?=CE・・・②

正解 :CD
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠?+∠ECD

正解 :ACE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠?+60°

正解 :ACE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠ACE+60°
∠BCE=∠ACB+∠ACE
=60°+∠ACE
よって
∠ACD=∠?・・・③

正解 :BCE
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠ACE+60°
∠BCE=∠ACB+∠ACE
=60°+∠ACE
よって
∠ACD=∠BCE・・・③
①、②、③より?ので
△ACD≡△BCE

正解 :2組の辺とその間の角がそれぞれ等しい。 (SAS)
この図の△ABCと△ECDは正三角形です。
線分AD、線分BEを引くときAD=BEとなることを証明しましょう。
△ACDと△BCEにおいて
△ABCと△ECDは正三角形なので
AC=BC・・・①
CD=CE・・・②
∠ECD=∠ACB=60°
ここで∠ACD=∠ACE+∠ECD
=∠ACE+60°
∠BCE=∠ACB+∠ACE
=60°+∠ACE
よって
∠ACD=∠BCE・・・③
①、②、③より2組の辺とその間の角がそれぞれ等しいので
△ACD≡△BCE
合同な図形の対応する?は等しいので
AD=BE

正解 :辺の長さ