2-5-1-5 性質を利用した証明②
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CE
となるようにとります。
このとき、CD=BEとなることを
証明しましょう。
(1)仮定はどれでしょう?(すべて)
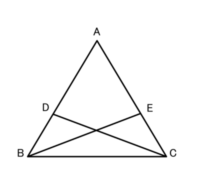
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
(1)仮定はどれでしょう?(すべて)
正解 :AB=ACの二等辺三角形,BD=CE
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
(2)結論はどれでしょう?(すべて)

正解 :CD=BE
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△?において

正解 :ECB
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△ECBにおいて
?よりBD=CE・・・①

正解 :仮定
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△ECBにおいて
仮定よりBD=CE・・・①
?なのでBC=CB・・・②

正解 :共通
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△ECBにおいて
仮定よりBD=CE・・・①
共通なのでBC=CB・・・②
?なので∠DBC=∠ECB・・・③

正解 :二等辺三角形の底角は等しい
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△ECBにおいて
仮定よりBD=CE・・・①
共通なのでBC=CB・・・②
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・③
①、②、③より?ので
△DBC≡△ECB

正解 :2組の辺とその間の角がそれぞれ等しい。 (SAS)
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,EをBD=CEとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DBCと△ECBにおいて
仮定よりBD=CE・・・①
共通なのでBC=CB・・・②
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・③
①、②、③より2組の辺とその間の角がそれぞれ等しいので
△DBC≡△ECB
合同な図形の対応する?は等しいので
CD=BE

正解 :辺
AB=ACの二等辺三角形ABCで、
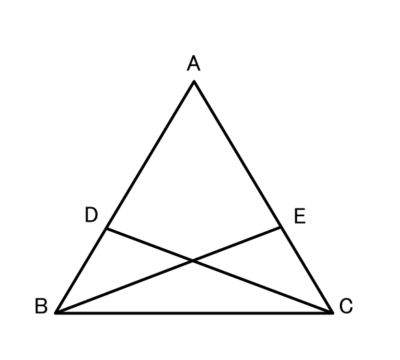
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
(1)仮定はどれでしょう?(すべて)

正解 :AB=ACの二等辺三角形,∠DCB=∠EBC
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
(2)結論はどれでしょう?(すべて)

正解 :CD=BE
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△?において

正解 :EBC
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△EBCにおいて
?より∠DCB=∠EBC・・・①

正解 :仮定
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△EBCにおいて
仮定より∠DCB=∠EBC・・・①
?なのでCB=BC・・・②

正解 :共通
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△EBCにおいて
仮定より∠DCB=∠EBC・・・①
共通なのでCB=BC・・・②
?なので∠DBC=∠ECB・・・③

正解 :二等辺三角形の底角は等しい
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△EBCにおいて
仮定より∠DCB=∠EBC・・・①
共通なのでCB=BC・・・②
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・③
①、②、③、より?ので
△DCB≡△EBC

正解 :1組の辺とその両端の角がそれぞれ等しい。 (ASA)
AB=ACの二等辺三角形ABCで、
辺AB,AC上に点D,Eを∠DCB=∠EBCとなるようにとります。
このとき、CD=BEとなることを証明しましょう。
△DCBと△EBCにおいて
仮定より∠DCB=∠EBC・・・①
共通なのでCB=BC・・・②
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・③
①、②、③、より1組の辺とその両端の角がそれぞれ等しいので
△DCB≡△EBC
合同な形の対応する?は等しいので
CD=BE

正解 :辺
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
(1)仮定はどれでしょう?(すべて)
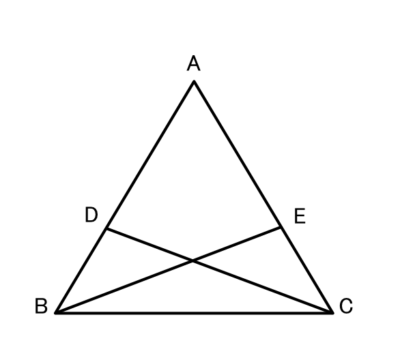
正解 :AB=AC,AE=AD
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
(2)結論はどれでしょう?(すべて)

正解 :BE=CD
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
どの三角形とどの三角形の合同を証明ができますか?
合同条件などから考えてみましょう。
正解 :△AEBと△ADC
この図でAB=AC、AE=ADならば、BE=CDであることを証明しましょう。
△AEBと△ADCにおいて
?よりAB=AC
正解 :仮定
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
△AEBと△ADCにおいて
仮定よりAB=AC・・・①
?よりAE=AD・・・②

正解 :仮定
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
△AEBと△ADCにおいて
仮定よりAB=AC・・・①
仮定よりAE=AD・・・②
?なので∠EAB=∠DAC・・・③

正解 :共通
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
△AEBと△ADCにおいて
仮定よりAB=AC・・・①
仮定よりAE=AD・・・②
共通なので∠EAB=∠DAC・・・③
①、②、③、より?なので
△AEB≡△ADC

正解 :2組の辺とその間の角がそれぞれ等しい。 (SAS)
この図でAB=AC、AE=ADならば、
BE=CDであることを証明しましょう。
△AEBと△ADCにおいて
仮定よりAB=AC・・・①
仮定よりAE=AD・・・②
共通なので∠EAB=∠DAC・・・③
①、②、③、より2組の辺とその間の角がそれぞれ等しいので
△AEB≡△ADC
合同な形の対応する?は等しいので
BE=CD

正解 :辺