2-4-7-2 合同を利用した証明
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなります。
(1)仮定はどれでしょうか?(すべて)
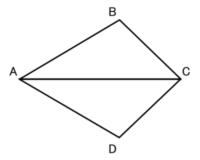
この図でAB=AD、CB=CDならば、∠ABC=∠ADCとなります。
(1)仮定はどれでしょうか?(すべて)
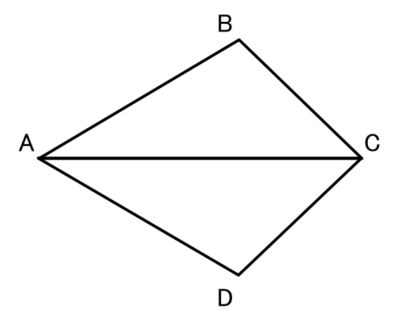
正解 :AB=AD,CB=CD
この図でAB=AD、CB=CDならば、∠ABC=∠ADCとなります。
(2)結論はどれでしょうか?(すべて)

正解 :∠ABC=∠ADC
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△?において

正解 :ADC
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△ADCにおいて
?よりAB=AD・・・①

正解 :仮定
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△ADCにおいて
仮定よりAB=AD・・・①
?よりCB=CD・・・②

正解 :仮定
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△ADCにおいて
仮定よりAB=AD・・・①
仮定よりCB=CD・・・②
?なのでCA=CA・・・③

正解 :共通
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△ADCにおいて
仮定よりAB=AD・・・①
仮定よりCB=CD・・・②
共通なのでCA=CA・・・③
①、②、③より?なので
△ABC≡△ADC

正解 :3組の辺がそれぞれ等しい。(SSS)
この図でAB=AD、CB=CDならば、
∠ABC=∠ADCとなることを証明します。
△ABCと△ADCにおいて
仮定よりAB=AD・・・①
仮定よりCB=CD・・・②
共通なのでCA=CA・・・③
①、②、③より3組の辺がそれぞれ等しいので
△ABC≡△ADC
合同な図形の対応する?は等しいので
∠ABC=∠ADC

正解 :角
この図でAB=AD、AC=AEならば、BC=DEとなります。
(1)仮定はどれでしょうか?(すべて)
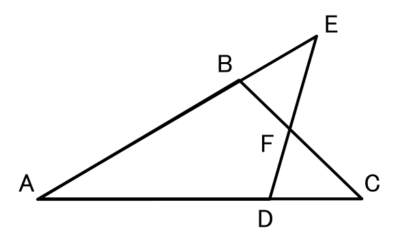
正解 :AB=AD,AC=AE
この図でAB=AD、AC=AEならば、BC=DEとなります。
(2)結論はどれでしょうか?(すべて)

正解 :BC=DE
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△?において
正解 :ADE
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△ADEにおいて
?よりAB=AD・・・①
正解 :仮定
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△ADEにおいて
仮定よりAB=AD・・・①
?よりAC=AE・・・②
正解 :仮定
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△ADEにおいて
仮定よりAB=AD・・・①
仮定よりAC=AE・・・②
?なので∠BAC=∠DAE・・・③
正解 :共通
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△ADEにおいて
仮定よりAB=AD・・・①
仮定よりAC=AE・・・②
共通なので∠BAC=∠DAE・・・③
①、②、③より?なので
△ABC≡△ADE
正解 :2組の辺とその間の角がそれぞれ等しい。 (SAS)
この図でAB=AD、AC=AEならば、
BC=DEとなることを証明しましょう。
△ABCと△ADEにおいて
仮定よりAB=AD・・・①
仮定よりAC=AE・・・②
?なので∠BAC=∠DAE・・・③
①、②、③より2組の辺とその間の角がそれぞれ等しいので
△ABC≡△ADE
合同な図形の対応する?は等しいので
BC=DE

正解 :辺
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
(1)仮定はどれでしょうか?(すべて)
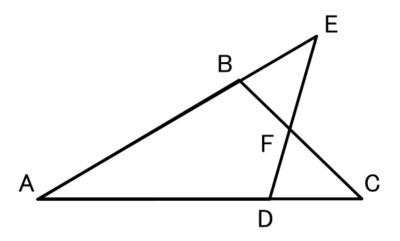
正解 :∠BEF=∠DCF,EF=CF
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
(2)結論はどれでしょうか?(すべて)
正解 :BF=DF
この図で∠BEF=∠DCF、EF=CFならば、BF=DFとなります。
△BEFと△?において

正解 :DCF
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
△BEFと△DCFにおいて
?より∠BEF=∠DCF・・・①

正解 :仮定
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
△BEFと△DCFにおいて
仮定より∠BEF=∠DCF・・・①
?よりEF=CF・・・②
正解 :仮定
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
△BEFと△DCFにおいて
仮定より∠BEF=∠DCF・・・①
仮定よりEF=CF・・・②
?より∠BFE=∠DFC・・・③
正解 :対頂角
この図で∠BEF=∠DCF、EF=CFならば、
BC=DEとなります。
△BEFと△DCFにおいて
仮定より∠BEF=∠DCF・・・①
仮定よりEF=CF・・・②
対頂角より∠BFE=∠DFC・・・③
①、②、③より?ので
△BEF≡△DCF
正解 :1組の辺とその両端の角がそれぞれ等しい。 (ASA)
この図で∠BEF=∠DCF、EF=CFならば、
BF=DFとなります。
△BEFと△DCFにおいて
仮定より∠BEF=∠DCF・・・①
仮定よりEF=CF・・・②
対頂角より∠BFE=∠DFC・・・③
①、②、③より1組の辺とその両端の角がそれぞれ等しいので
△BEF≡△DCF
合同な三角形の対応する?は等しいので
BF=DF
正解 :辺