2-3-4-9 混合問題
問題 1次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
傾きが -3 で、切片が 2 である直線。
正解 :-3x+2
問題 2次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
変化の割合が 12で、切片が 2 である直線。
2
正解 :1,2,2
問題 3次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
傾きが 1 で、(0,0)を通る直線。
正解 :x
問題 4次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
変化の割合が -2 で x=2のとき y=3 である1次関数。
正解 :-2x+7
問題 5次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
変化の割合が -3 で (2,1)を通る1次関数。
正解 :-3x+7
問題 6次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
変化の割合が 3 で (1,1)を通る1次関数。
正解 :3x-2
問題 7次の条件の1次関数の式を求めましょう。
次の条件の1次関数の式を求めましょう。
y=-2x+1と平行 で x=2のとき y=3 である1次関数。(y=ax+b)
正解 :-2x+7
問題 8次の条件の1次関数の式を求めましょう。
次の条件の1次関数の式を求めましょう。
y=-3x+1と平行 で (2,1)を通る1次関数。(y=ax+b)
正解 :-3x+5
問題 9次の条件の1次関数の式を求めましょう。
次の条件の1次関数の式を求めましょう。
y=-3x-9 と平行で x=-1のとき y=1 である1次関数。(y=ax+b)
正解 :-3x-2
問題 10次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
切片が -3 で x=-1 のとき y=-2 である1次関数。
正解 :-x-3
問題 11次の条件の1次関数の式(y=ax+b)を求めましょう。
次の条件の1次関数の式(y=ax+b)を求めましょう。
切片が 1 で (-1,2) を通る1次関数。
正解 :-x+1
問題 12直線 y=-x+2 に平行で、
直線 y=-x+2 に平行で、
直線 y=-2xと y 軸上で交わる直線を求めましょう。(y=ax+b)
正解 :-x
問題 13直線 y=3x+9 に平行で、
直線 y=3x+9 に平行で、
直線 y=-x+13と y 軸上で交わる直線を求めましょう。(y=ax+b)
正解 :3x+13
問題 14直線 y=x+5 に平行で、
直線 y=x+5 に平行で、
直線 y=-xと y 軸上で交わる直線を求めましょう。(y=ax+b)
正解 :x
問題 15
2点(2,3), (-2,5)を通る直線の式を求めましょう。(y=ax+b)
正解 :1,2,4,
問題 16
x=1 のとき y=3, x=-2 のとき y=0 である1次関数を求めましょう。(y=ax+b)
正解 :x+2
問題 17
対応する x,y の関係がこの表のようになる1次関数の式を求めましょう。
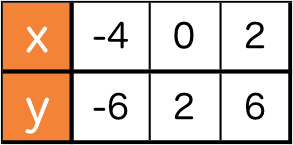
正解 :2x+2
問題 18
対応する x,y の関係がこの表のようになる1次関数の式を求めましょう。

正解 :-3x+3
問題 19
対応する x,y の関係がこの表のようになる1次関数の式を求めましょう。
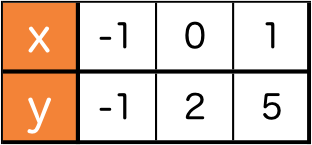
正解 :3x+2