2-5-4-4 直角三角形の合同条件を利用した証明
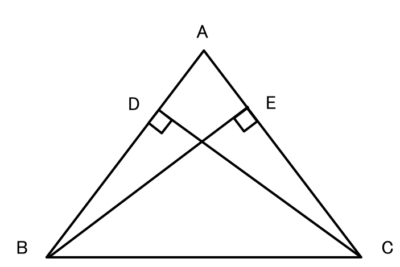
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと?において
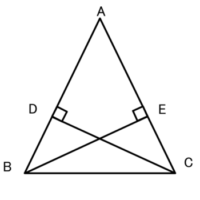
問題 1AB=AC である二等辺三角形 ABC において、
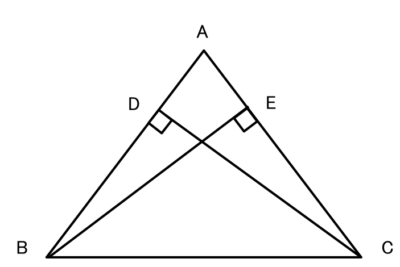
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと?において
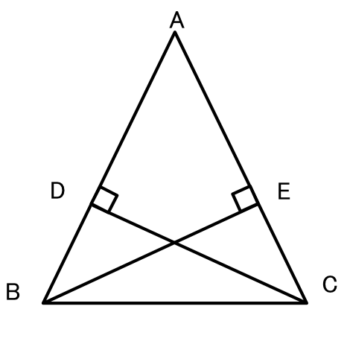
正解 :ACD
問題 2AB=AC である二等辺三角形 ABC において、
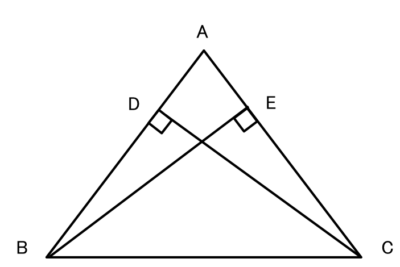
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと△ACDにおいて
?より∠AEB=∠ADC=90・・・①
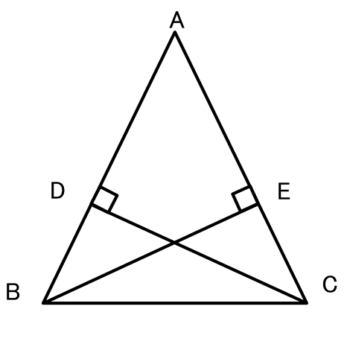
正解 :仮定
問題 3AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと△ACDにおいて
仮定より∠AEB=∠ADC=90・・・①
?よりAB=AC
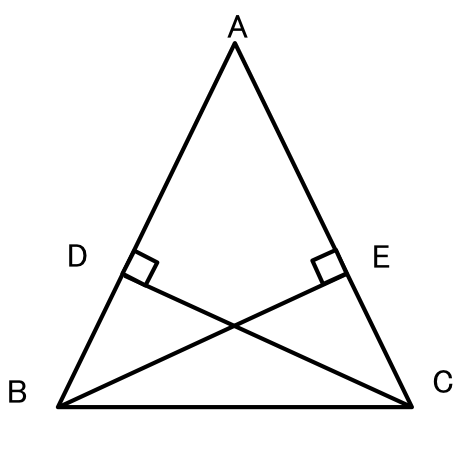
正解 :仮定
問題 4AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと△ACDにおいて
仮定より∠AEB=∠ADC=90・・・①
仮定よりAB=AC・・・②
?なので∠EAB=∠DAC・・・③

正解 :共通
問題 5AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このとき△ABEと△ACDであることを証明しましょう。
△ABEと△ACDにおいて
仮定より∠AEB=∠ADC=90・・・①
仮定よりAB=AC・・・②
共通なので∠EAB=∠DAC・・・③
①、②、③より?ので
△ABE≡△ACD

正解 :直角三角形の斜辺と1つの鋭角がそれぞれ等しい。(RHA)
問題 6AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
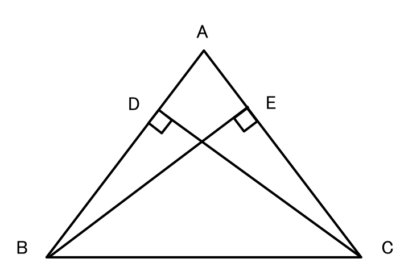
頂点B、Cから、AC、ABに垂線をひく。
このときDB=ECであることを証明しましょう。
△DBCと△ECBにおいて
?より∠BDC=∠CEB・・・①
正解 :仮定
問題 7AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このときDB=ECであることを証明しましょう。
△DBCと△ECBにおいて
仮定より∠BDC=∠CEB・・・①
?ので∠DBC=∠ECB・・・②
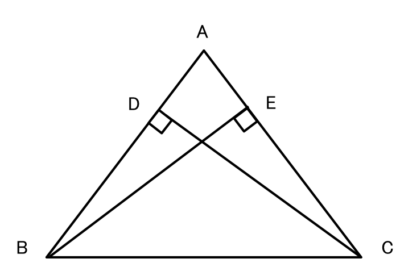
正解 :二等辺三角形の底角は等しい
問題 8AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このときDB=ECであることを証明しましょう。
△DBCと△ECBにおいて
仮定より∠BDC=∠CEB・・・①
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・②
?なのでBC=CB・・・③
正解 :共通
問題 9AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。
このときDB=ECであることを証明しましょう。
△DBCと△ECBにおいて
仮定より∠BDC=∠CEB・・・①
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・②
共通なのでBC=CB・・・③
①、②、③より?なので
△DBC≡△ECB
正解 :直角三角形の斜辺と1つの鋭角がそれぞれ等しい。(RHA)
問題 10AB=AC である二等辺三角形 ABC において、
AB=AC である二等辺三角形 ABC において、
頂点B、Cから、AC、ABに垂線をひく。このときDB=ECであることを証明しましょう。
△DBCと△ECBにおいて
仮定より∠BDC=∠CEB・・・①
二等辺三角形の底角は等しいので∠DBC=∠ECB・・・②
?なのでBC=CB・・・③
①、②、③より直角三角形の斜辺と他の1辺がそれぞれ等しいので
△DBC≡△ECB
合同な図形の対応する?は等しいので
DB=EC
正解 :辺
問題 11この図でAD=CD、∠BAD=∠BCD=90°であるとき
この図でAD=CD、∠BAD=∠BCD=90°であるとき
△ABDと△CBDが合同であることを証明しましょう。
△ABDと?において

正解 :CBD
問題 12この図でAD=CD、∠BAD=∠BCD=90°であるとき
この図でAD=CD、∠BAD=∠BCD=90°であるとき
△ABDと△CBDが合同であることを証明しましょう。
△ABDと△CBDにおいて
?よりAD=CD・・・①

正解 :仮定
問題 13この図でAD=CD、∠BAD=∠BCD=90°であるとき
この図でAD=CD、∠BAD=∠BCD=90°であるとき
△ABDと△CBDが合同であることを証明しましょう。
△ABDと△CBDにおいて
仮定よりAD=CD・・・①
?より∠BAD=∠BCD=90°・・・②
正解 :仮定
問題 14この図でAD=CD、∠BAD=∠BCD=90°であるとき
この図でAD=CD、∠BAD=∠BCD=90°であるとき
△ABDと△CBDが合同であることを証明しましょう。
△ABDと△CBDにおいて
仮定よりAD=CD・・・①
仮定より∠BAD=∠BCD=90°・・・②
?なのでBD=BD・・・③

正解 :共通
問題 15この図でAD=CD、∠BAD=∠BCD=90°であるとき
この図でAD=CD、∠BAD=∠BCD=90°であるとき
△ABDと△CBDが合同であることを証明しましょう。
△ABDと△CBDにおいて
仮定よりAD=CD・・・①
仮定より∠BAD=∠BCD=90°・・・②
共通なのでBD=BD・・・③
①、②、③より?なので
△ABD≡△CBD

正解 :直角三角形の斜辺と他の1辺がそれぞれ等しい。(RHS)