2-5-1-6 二等辺三角形になる三角形の証明
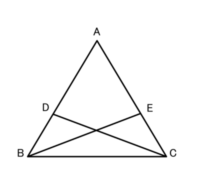
この図で、
△ABCの辺AB,AC上に
それぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは
二等辺三角形になることを証明しましょう。
(1)仮定はどれですか?(すべて)
この図で、
△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
(1)仮定はどれですか?(すべて)
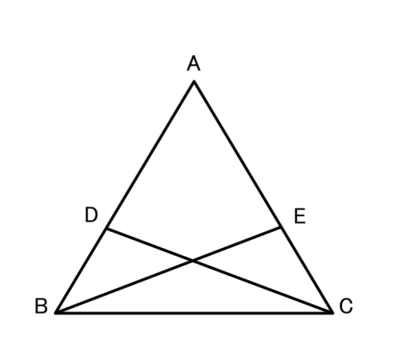
正解 :DC=EB,DB=EC
この図で、
△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
(2)結論はどれですか?(すべて)
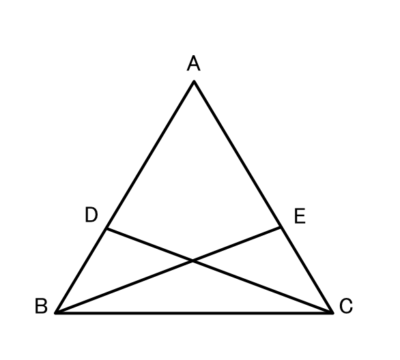
正解 :ABCは二等辺三角形
この図で、△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△?において
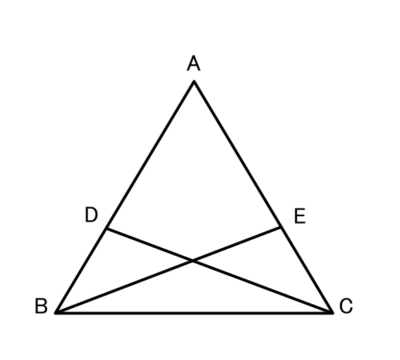
正解 :ECB
この図で、△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△ECBにおいて
?よりDB=EC
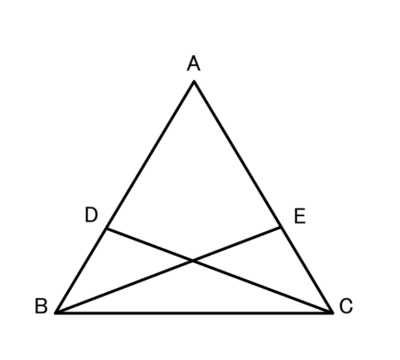
正解 :仮定
この図で、△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△ECBにおいて
仮定よりDB=EC・・・①
?よりDC=EB・・・②
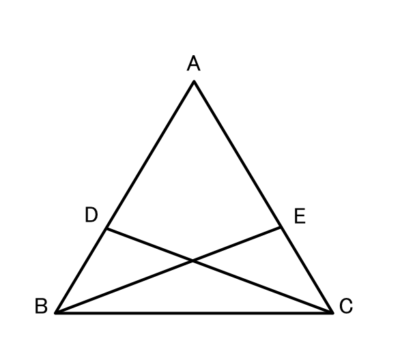
正解 :仮定
この図で、△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△ECBにおいて
仮定よりDB=EC・・・①
仮定よりDC=EB・・・②
?なのでBC=CB・・・③

正解 :共通
この図で、
△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△ECBにおいて
仮定よりDB=EC・・・①
仮定よりDC=EB・・・②
共通なのでBC=CB・・・③
①、②、③より?なので
△DBC≡△ECB

正解 :3組の辺がそれぞれ等しい。(SSS)
この図で、
△ABCの辺AB,AC上にそれぞれDB=ECとなるように点D,Eをとる。
DC=EBのとき、△ABCは二等辺三角形になることを証明しましょう。
△DBCと△ECBにおいて
仮定よりDB=EC・・・①
仮定よりDC=EB・・・②
共通なのでBC=CB・・・③
①、②、③より?なので
△DBC≡△ECB
合同な三角形の対応する角は等しいので
?=?
したがって2つの角が等しいので、△ABCは二等辺三角形になる。

正解 :∠DBC=∠ECB
この図で、
△ABCの辺AB,AC上にそれぞれAD=AEとなるように点D,Eをとる。
∠ADC=∠AEBのとき、△ABCは二等辺三角形になることを証明しましょう。
(1)どの三角形とどの三角形の合同の証明を使うでしょうか?

正解 :△ADCと△AEB
この図で、
△ABCの辺AB,AC上にそれぞれAD=AEとなるように点D,Eをとる。
∠ADC=∠AEBのとき、△ABCは二等辺三角形になることを証明しましょう。
△ADCと△AEBにおいて
仮定よりAD=AE・・・①
仮定より∠ADC=∠AEB・・・②
共通なので?=?・・・③

正解 :∠DAC=∠EAB
この図で、
△ABCの辺AB,AC上にそれぞれAD=AEとなるように点D,Eをとる。
∠ADC=∠AEBのとき、△ABCは二等辺三角形になることを証明しましょう。
△ADCと△AEBにおいて
仮定よりAD=AE・・・①
仮定より∠ADC=∠AEB・・・②
共通なので∠DAC=∠EAB・・・③
①、②、③より?ので
△ADC≡△AEB

正解 :1組の辺とその両端の角がそれぞれ等しい。 (ASA)
この図で、
△ABCの辺AB,AC上にそれぞれAD=AEとなるように点D,Eをとる。
∠ADC=∠AEBのとき、△ABCは二等辺三角形になることを証明しましょう。
△ADCと△AEBにおいて
仮定よりAD=AE・・・①
仮定より∠ADC=∠AEB・・・②
共通なので∠DAC=∠EAB・・・③
①、②、③より1組の辺とその両端の角がそれぞれ等しいので
△ADC≡△AEB
合同な三角形の対応する辺は等しいので
?=?

正解 :AC=AB
この図で、△ABCの辺AB,AC上にそれぞれAD=AEとなるように点D,Eをとる。
∠ADC=∠AEBのとき、△ABCは二等辺三角形になることを証明しましょう。
△ADCと△AEBにおいて
仮定よりAD=AE・・・①
仮定より∠ADC=∠AEB・・・②
共通なので∠DAC=∠EAB・・・③
①、②、③より1組の辺とその両端の角がそれぞれ等しいので
△ADC≡△AEB
合同な三角形の対応する辺は等しいので
AC=AB
したがって?は等しいので△ABCは二等辺三角形である。

正解 :2つの辺