3-5-3-1 相似の証明
この図について、△ABCと△EDCが
相似になることを証明しましょう。
△ABCと△EDCにおいて
?より∠ABC=∠EDC・・・①
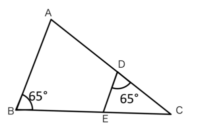
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
?より∠ABC=∠EDC・・・①
正解 :仮定
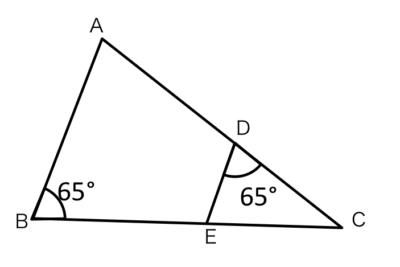
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より∠ABC=∠EDC・・・①
共通なので∠BCA=∠?・・・②

正解 :DCE
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より∠ABC=∠EDC・・・①
共通なので∠BCA=∠DCE・・・②
①、②より?なので
△ABC∽△EDC

正解 :2組の角がそれぞれ等しい
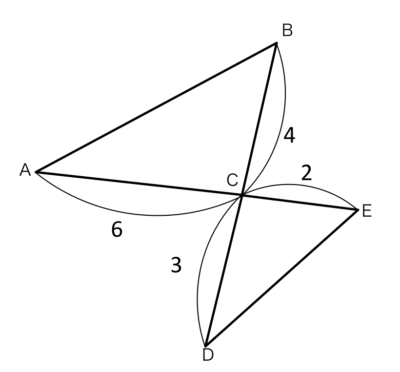
この図について、△ABCと△DECが相似になることを証明しましょう。
△ABCと△DECにおいて
仮定より AC:DC=6:3=?:?・・・①
正解 :2,1
この図について、△ABCと△DECが相似になることを証明しましょう。
△ABCと△DECにおいて
仮定より AC:DC=6:3=2:1・・・①
仮定より BC:EC=4:2=?:?・・・②

正解 :2,1
この図について、△ABCと△DECが相似になることを証明しましょう。
△ABCと△DECにおいて
仮定より AC:DC=6:3=2:1・・・①
仮定より BC:EC=4:2=2:1・・・②
対頂角なので ∠ACB=∠?・・・③

正解 :DCE
この図について、△ABCと△DECが相似になることを証明しましょう。
△ABCと△DECにおいて
仮定より AC:DC=6:3=2:1・・・①
仮定より BC:EC=4:2=2:1・・・②
対角線なので ∠ACB=∠DCE・・・③
①、②、③より?なので
△ABC∽△DEC

正解 :2組の辺の比とその間の角がそれぞれ等しい
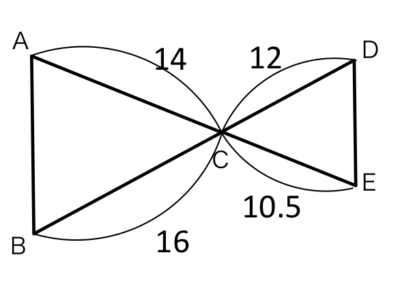
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より BC:DC=16:12=?:?・・・①
正解 :4,3
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より BC:DC=16:12=4:3・・・①
仮定より AC:EC=14:10.5=?:?・・・②

正解 :4,3
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より BC:DC=16:12=4:3・・・①
仮定より AC:EC=14:10.5=4:3・・・②
?なので∠ACB=∠ECD・・・③

正解 :対頂角
この図について、△ABCと△EDCが相似になることを証明しましょう。
△ABCと△EDCにおいて
仮定より BC:DC=16:12=4:3・・・①
仮定より AC:EC=14:10.5=4:3・・・②
対頂角なので∠ACB=∠ECD・・・③
①、②、③より?なので
△ABC∽△EDC

正解 :2組の辺の比とその間の角がそれぞれ等しい
この図について、△ABCと△DBAが相似になることを証明しましょう。
△ABCと△DBAにおいて
仮定より AB:DB=6:8=?:?・・・①
正解 :3,4
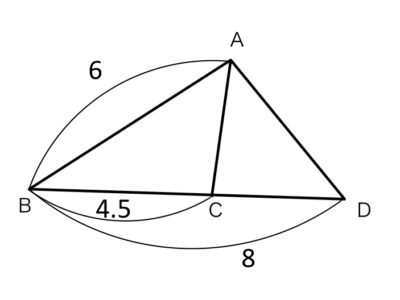
この図について、△ABCと△DBAが相似になることを証明しましょう。
△ABCと△DBAにおいて
仮定より AB:DB=6:8=3:4・・・①
仮定より BC:BA=4.5:6=?:?・・・②

正解 :3,4
この図について、△ABCと△DBAが相似になることを証明しましょう。
△ABCと△DBAにおいて
仮定より AB:DB=6:8=3:4・・・①
仮定より BC:BA=4.5:6=3:4・・・②
?なので∠ABC=∠DBA・・・③

正解 :共通
この図について、△ABCと△DBAが相似になることを証明しましょう。
△ABCと△DBAにおいて
仮定より AB:DB=6:8=3:4・・・①
仮定より BC:BA=4.5:6=3:4・・・②
共通なので∠ABC=∠DBA・・・③
①、②、③より?ので
△ABC∽△DBA

正解 :2組の辺の比とその間の角がそれぞれ等しい